TuLiP planning, May 2013: Difference between revisions
No edit summary |
|||
| Line 39: | Line 39: | ||
# The <tt>ptolemy</tt> module contains functions for interfacing with Ptolemy. | # The <tt>ptolemy</tt> module contains functions for interfacing with Ptolemy. | ||
#* Should we instead make an FMI interface and then use Ptolemy's FMI capability? --[[User:Murray|Richard Murray]] ([[User talk:Murray|talk]]) 15:09, 11 May 2013 (PDT) | #* Should we instead make an FMI interface and then use Ptolemy's FMI capability? --[[User:Murray|Richard Murray]] ([[User talk:Murray|talk]]) 15:09, 11 May 2013 (PDT) | ||
#* We should be careful about MoC the automaton is synthesized for (event-based, discrete-time, continuous-time etc.) while interfacing. Ptolemy and FMI seem to have better support for certain types. -- Necmiye | |||
# It would be nice to have transition system class support symbolic representations (e.g., based on variable tuples as is now instead of listing all states). For instance for a 10x10 grid, one might want to define the problem in terms of x and y coordinates instead of listing 100 states. Another example where listing the states is difficult is vms examples, where we have temperature, ice_level, wind_level, etc. This way we can take better advantage of underlying symbolic computations. -- Necmiye | |||
=== Create a discrete example from scratch === | === Create a discrete example from scratch === | ||
Revision as of 17:14, 12 May 2013
This page contains a draft description of the TuLiP toolbox.
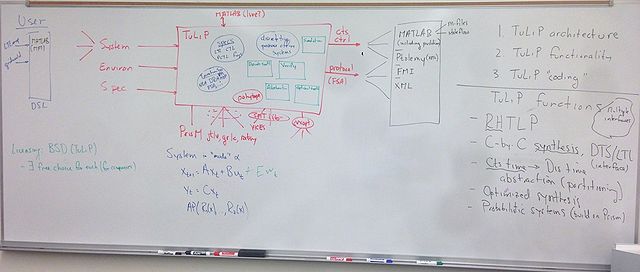
Architecture
Notes from 30 April 2013 meeting:
Examples
This section contains a set of example that illustrate how the TuLiP code should be structured. This goes first so that we focus on the TuLiP interface and functionality and then figure out what is required to support it.
Load up an example stored in files and synthesize a controller
This example shows how to load up a problem that is specified in files and synthesize a controller. Save the controller to a file, but also generate a version that can be executed in Ptolemy.
Code
import tulip
# Load up the system and environment descriptions, plus specifications
system = tulip.ts.load("robot-discrete.tsf")
environment = tulip.sp.load("robot-env.spf")
specs = tulip.sp.load("robot-specs.spf")
# Synthesize a controller
controller = tulip.syn.jtlv(system, environment, specs)
# Save the controller in TuLiP and Ptolemy formats
tulip.ts.save("robot-control.tsf")
tulip.ptolemy.savefsm("robot-control.fsm")
Notes
- The .tsf (transition system file) and .spf (specification file) formats are the default TuLiP file formats.
- Alternatively, perhaps we have a single file format .tlp and then use tulip.load and tulip.save to read and write. The type of object would just be part of the file specification. --Richard Murray (talk) 15:07, 11 May 2013 (PDT)
- The tf module contains data types and functions for representing different types of transition systems. Multiple transition systems are supported, including deterministic transition systems, Markov decision processes, Kripke structures, Rabin automata, etc.
- The sp module contains data types and functions for representing specifications. Multiple temporal logics, including LTL, MTL, CTL, PCTL, TCTL, STL, etc are supported.
- The syn module contains interfaces to various synthesis tools. Supported tools include JTLV, gr1c and PRISM. The input arguments must be compatible with the synthesis tool, but all arguments should be core TuLiP objects.
- Would it make more sense to have a module for each program we support? So this line would become tulip.jtlv.syn? --Richard Murray (talk) 15:07, 11 May 2013 (PDT)
- The ptolemy module contains functions for interfacing with Ptolemy.
- Should we instead make an FMI interface and then use Ptolemy's FMI capability? --Richard Murray (talk) 15:09, 11 May 2013 (PDT)
- We should be careful about MoC the automaton is synthesized for (event-based, discrete-time, continuous-time etc.) while interfacing. Ptolemy and FMI seem to have better support for certain types. -- Necmiye
- It would be nice to have transition system class support symbolic representations (e.g., based on variable tuples as is now instead of listing all states). For instance for a 10x10 grid, one might want to define the problem in terms of x and y coordinates instead of listing 100 states. Another example where listing the states is difficult is vms examples, where we have temperature, ice_level, wind_level, etc. This way we can take better advantage of underlying symbolic computations. -- Necmiye
Create a discrete example from scratch
This example shows how to create a system and environment from scratch, then synthesize a controller. It is based on the robot-simple.py example that is distributed with TuLiP and used in the EECI short course.
Code
import tulip
#
# Create the system transition system corresponding to a 2x3 grid of cells
#
system = tulip.ts()
system.addstates({'c11', 'c12', 'c13', 'c21', 'c22', 'c23'})
# Allow transitions between adjacent cells
system.addtransition('c11', True, {'c12', 'c21'})
system.addtransition('c12', True, {'c11', 'c13', 'c22'})
system.addtransition('c13', True, {'c12', 'c31'}})
system.addtransition('c21', True, {'c12', 'c22'})
system.addtransition('c22', True, {'c21', 'c23', 'c12'})
system.addtransition('c23', True, {'c22', 'c13'}})
# Add labels to selected points
system.addlabel('home', 'c11')
system.addlabel('lot', 'c13 or c23')
#
# Create an environment that allows an obstacle to move around in the same state space
#
# We model the environment in a slightly different way, just to show functionality
#
environment = tulip.ts()
environment.addvar('obs', system.states)
envspec = tulip.spec(environment,
( obs = c11 -> next (obs = c12 or obs = c21) ) and
( obs = c12 -> next (obs = c11 or obs = c13 or obs = c22) ) and
( obs = c13 -> next (obs = c12 or obs = c31) ) and
( obs = c21 -> next (obs = c22 or obs = c12) ) and
( obs = c22 -> next (obs = c21 or obs = c23 or obs = c12) ) and
( obs = c23 -> next (obs = c22 or obs = c13) )
')
environment.addvar('park', {1, 0})
envspec = envspec + tulip.spec(environment, '[] <> !park')
#
# System specification
#
spec = tulip.spec({system,environment}, envspec + '->
(always eventually home) and
(always (park -> eventually lot)) and
(always !(
(obs = c11 and c11) or
(obs = c12 and c12) or
(obs = c13 and c13) or
(obs = c21 and c21) or
(obs = c22 and c22) or
(obs = c23 and c23) ) )
')
# Synthesize the automaton
controller = tulip.syn.jtlv(system, environment, spec)
# Simulate the system
Discretize continuous dynamics
import tulip
import control
# Create a hybrid system with 2D continuous space and no discrete dynamics
system = tulip.hybrid(2, {})
# Define the dynamics for the system
sysdyn = control.ss({{0,0,1,0}, {0,0,0,1}, {0, 0, 0, 0}, {0,0,0,0}}, {{0,0}, {0,0}, {1,0}, {0,1}}, {{1,0,0,0}, {0,1, 0,0}}, 0)
# Define the regions for the system, along with labels and dynamics
system.addregion({{0,0}, {1,1}}, 'c11', sysdyn)
system.addregion({{1,0}, {2,1}}, 'c12', sysdyn)
system.addregion({{2,0}, {3,1}}, 'c13', sysdyn)
system.addregion({{0,1}, {1,2}}, 'c21', sysdyn)
system.addregion({{1,1}, {2,2}}, 'c22', sysdyn)
system.addregion({{2,1}, {3,2}}, 'c23', sysdyn)
# Discretize the dynamics
tulip.discretize(system, 0.01)
TuLiP classes
TransitionSystem
A transition system consists of
- states - a list of elements that correspond to the states of the system. Elements are nominally strings
- transitions - optional subset of states x states indicating allowable transitions (doesn't have to be deterministic)
- actions - list of actions and what transitions they enable. If empty
- labels - list of atomic propositions for any subsets of states. Atomic propositions are given by set of all label outputs
- initial states
- acceptance sets - for Buchi and Rabin automata
Available functions
Specification
A specification is a temporal logic formula. Specifications can be input and output as strings using the following symbols:
- state - evaluates to true if the system is in the discrete state
- atomic - evaluates to true if the atomic proposition is true
- logical operators: and, or, not, implies, &, ^, !, ->
- comparison operators: =, <=, >=, !=
- temporal operators: always, eventually, until, next, [], <>, U, X
- path operators: forall, exists, F, E
- probability operators?
HybridSystem
The HybridSystem class is used to define systems that have continuous time dynamics. The state space of a hybrid system can be continuous, discrete or both.
A space system consists of
- discrete state space - set of discrete states
- continuous state space - list of polygonal regions that are each subsets of R^n
- discrete inputs - set of discrete inputs that affect evolution of the system
- continuous inputs - set of continuous inputs that affect evolution of the system
- discrete transitions - set of guarded commands
- continuous dynamics - for each polygonal region, a set of dynamics that define the evolution of the system (given values for the inputs)