SURF 2014: Improved methods of discretization for temporal logic planning
2014 SURF project description
- Mentor: Richard M. Murray
- Co-mentor: Yilin Mo
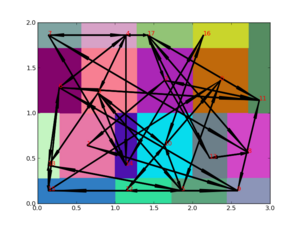
The Temporal Logic Planning Toolbox, TuLiP, is a collection of Python-based routines for automatic synthesis of correct-by-construction embedded control software as discussed in [1]. To this end, TuLiP converts a control system to a finite transition system by discretizing the continuous control space (typically a high dimensional rectangle) into finitely many polytopes, each of which represents a state of the finite transition system[2]. The discretization algorithm is based on the specifications of the system and reachability analysis. Fig 1 illustrates the discretization of a rectangle into 19 small rectangles. The arrows between rectangles indicate possible transitions from one rectangle to the other.
Two issues remain in the current algorithm:
- The discretization algorithm may fail to converge to a solution.
- It is unclear whether the discretization algorithms will generate the optimal collection of polytopes, which is the most efficient one for the synthesis purpose.
This project aims at:
- providing a formal proof on the convergence of the discretization algorithm;
- developing a benchmark to quantify the efficiency of the discretization algorithm.
Along with this study, it is expected that the theoretical development of the discretization algorithm will also be integrated into TuLiP.
Required skills: The student should be familiar with basic control theory. In addition, this project requires programming experience. The programming language underlying TuLiP is Python. The student is expected to know Python or to have enough programming experience to learn it in a short time. Some familiarity with or willingness to learn automata theory, formal languages, and model checking is desired.
References
[1] T. Wongpiromsarn, U. Topcu, N. Ozay, H. Xu, and R.~M. Murray, TuLiP: a software toolbox for receding horizon temporal logic planning, International Conference on Hybrid Systems: Computation and Control, 2011 (software available at: https://github.com/tulip-control/tulip-control).
[2] T. Wongpiromsarn, U. Topcu, and R. Murray. Receding horizon temporal logic planning. Automatic Control, IEEE Transactions on, 57(11):2817-2830, 2012.