SURF 2015: Optimal Trajectory Generation under Environmental Uncertainties using Signal Temporal Logic Specifications: Difference between revisions

From Murray Wiki
Jump to navigationJump to search
No edit summary
No edit summary
Line 3: Line 3:
* Co-mentor: Samira Farahani
* Co-mentor: Samira Farahani


The recent planetary decadal survey describes missions that impose tremendously challenging requirements on resilience. The Uninhabited Aerial Vehicles (UAVs) and spacecraft that support these missions will need to be capable of reasoning about their own state and the state of the environment in order to predict and avoid hazardous conditions, to recover from internal failures, and to ultimately meet critical science objectives in the presence of substantial uncertainties.  
In safety-critical robotics applications in which autonomous air, ground, and space vehicles carry out complex tasks, it is important to concisely and unambiguously specify the desired system behavior to be able to automatically synthesize a controller that implements this behavior. Controller synthesis is complicated by the fact that autonomous systems often have high-dimensional, nonlinear dynamics and require efficient (not just feasible) controllers.  


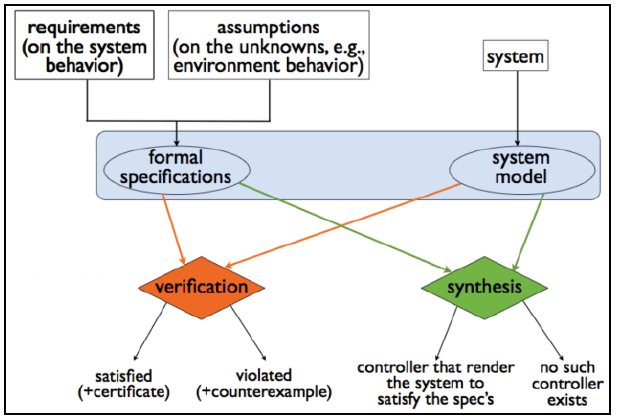
This project aims at designing a “correct by construction” controller for a UAV to satisfy its mission under the environmental uncertainties. To this end, we will take advantage of the new tools and techniques for formal specification, design, and verification of embedded control systems [1,2,3,4]. In these approaches, we either verify that a given design satisfies the specification or synthesize a controller that satisfies the specification, as summarized in the following figure.  
This project aims at designing a “correct by construction” controller for an autonomous vehicle that is capable of responding to a dynamic environment, visiting goals, periodically monitoring areas, staying safe, and remaining stable. To this end, we will take advantage of the new tools and techniques for formal specification, design, and verification of embedded control systems [3,4,5,7]. In these approaches, we either verify that a given design satisfies the specification or synthesize a controller that satisfies the specification, as summarized in the following figure.  


Once the model is designed and tested using computer simulation, it is going to be implemented on one of the UAVs that are available in our lab. The idea is to use this UAV as a benchmark to experiment the effect of environmental changes on the controller and to investigate the responsiveness of the controller to these changes.  
The formal language that we use in this project is Signal Temporal Logic (STL), which allows the specification of properties of dense-time, real-valued signals. For an efficient implementation, we will directly encode an STL formula as mixed-integer linear constraints on the original dynamical system [6]. Of particular interest are mixed logical dynamical (MLD) systems and certain differentially flat systems [2], whose dynamics can be encoded with mixed-integer linear constraints. MLD systems include constrained linear systems, linear hybrid automata, and piecewise affine systems. Differentially flat systems include quadrotors and car-like robots.
 
After the successful design the controller, we are going to perform a detailed comparison of mixed-integer linear programming solvers and Boolean satisfiability solvers that have been extended to support linear operations, e.g., [1]. Moreover, depending on the progress lever, we can also implement the controller on of the available robots in the lab for experimental purposes.  


[[File:Agent.png]]
[[File:Agent.png]]


''Required Skills:'' The software we will use for the implementation of formal methods is called TuLiP [5] and the programming language underlying TuLiP is Python. The student is expected to know Python or to have enough programming experience to learn it in a short time. Some familiarity with or willingness to learn automata theory, formal languages, and model checking (see for instance to the extent of the first 5 lectures in [6]) is desired.
''Required Skills:'' The software we will use for the implementation of formal methods is called TuLiP [5] and the programming language underlying TuLiP is Python. The student is expected to know Matlab and Python or to have enough programming experience to learn it in a short time. Some familiarity with or willingness to learn automata theory, formal languages, and model checking (see for instance to the extent of the first 5 lectures in [6]) is desired.


References:
References:


[1] S. Livingston, R. M. Murray, and J. W. Burdick. Backtracking temporal logic synthesis for uncertain environments. In Proc. IEEE International Conference on Robotics and Automation, 2012.
[1] M. Fränzle and C. Herde. Efficient proof engines for bounded model checking of hybrid systems. Electronic Notes in Theoretical Computer Science, 133:119–137, 2005.
http://homepage.divms.uiowa.edu/~tinelli/classes/AR-group/readingsF04/FMICS04_Fraenzle_Herde.pdf
 
[2] S. M. LaValle. Planning Algorithms. Cambridge Univ. Press, 2006.
http://planning.cs.uiuc.edu/bookbig.pdf
 
[3] S. Livingston, R. M. Murray, and J. W. Burdick. Backtracking temporal logic synthesis for uncertain environments. In Proc. IEEE International Conference on Robotics and Automation, 2012.
http://scottman.net/pub/Livingston-Murray-Burdick-ICRA2012.pdf
http://scottman.net/pub/Livingston-Murray-Burdick-ICRA2012.pdf


[2] U. Topcu, N. Ozay, J. Liu, , and R. M. Murray. On synthesizing robust discrete controllers under modeling uncertainty. In Hybrid Systems: Computation and Control, 2012.
[4] U. Topcu, N. Ozay, J. Liu, , and R. M. Murray. On synthesizing robust discrete controllers under modeling uncertainty. In Hybrid Systems: Computation and Control, 2012.
http://www.cds.caltech.edu/~murray/preprints/tolm12-hscc_s.pdf
http://www.cds.caltech.edu/~murray/preprints/tolm12-hscc_s.pdf


[3] E. M. Wolff, U. Topcu, and R. M. Murray. Robust control of uncertain Markov decision processes with temporal logic speci_cations. In Proc. American Control Conference, 2012.
[5] E. M. Wolff, U. Topcu, and R. M. Murray, Optimization-based trajectory generation with linear temporal logic specifications, International Conference on Robotics and Automation (ICRA), 2014.  
http://www.cds.caltech.edu/~ewolff/wolff_cdc12.pdf
http://www.cds.caltech.edu/~ewolff/wolff_icra14.pdf
 
[6] V. Raman, A. Donzé, M. Maasoumy, R. M. Murray, A. Sangiovanni-Vincentelli, S. A. Seshia, Model Predictive Control with Signal Temporal Logic Specifications, CDC 2014.
http://users.cms.caltech.edu/~vasu/papers/vraman_cdc_14.pdf


4] T. Wongpiromsarn, U. Topcu, and R. M. Murray. Receding horizon temporal logic planning. IEEE Transactions on Automatic Control, 57(11):2817{2830, 2012. http://www.seas.upenn.edu/~utopcu/pubs/WTM-itac12.pdf
[7] T. Wongpiromsarn, U. Topcu, and R. M. Murray. Receding horizon temporal logic planning. IEEE Transactions on Automatic Control, 57(11):2817{2830, 2012. http://www.seas.upenn.edu/~utopcu/pubs/WTM-itac12.pdf


[5] Wongpiromsarn, U. Topcu, N. Ozay, H. Xu, and R.~M. Murray, TuLiP: a software toolbox for receding horizon temporal logic planning, International Conference on Hybrid Systems: Computation and Control, 2011 (software available at http://tulip-control.sourceforge.net).
[8] Wongpiromsarn, U. Topcu, N. Ozay, H. Xu, and R.~M. Murray, TuLiP: a software toolbox for receding horizon temporal logic planning, International Conference on Hybrid Systems: Computation and Control, 2011 (software available at http://tulip-control.sourceforge.net).
http://www.aero.umd.edu/~mumu/files/wtoxm_HSCC2011.pdf
http://www.aero.umd.edu/~mumu/files/wtoxm_HSCC2011.pdf


[6] EECI, "Specification, Design, and Verification of Distributed Embedded Systems" course website
[9] EECI, "Specification, Design, and Verification of Distributed Embedded Systems" course website
http://www.cds.caltech.edu/~murray/wiki/index.php/HYCON-EECI,_Spring_2013
http://www.cds.caltech.edu/~murray/wiki/index.php/HYCON-EECI,_Spring_2013

Revision as of 02:17, 29 December 2014

2015 SURF project description

  • Mentor: Richard Murray
  • Co-mentor: Samira Farahani

In safety-critical robotics applications in which autonomous air, ground, and space vehicles carry out complex tasks, it is important to concisely and unambiguously specify the desired system behavior to be able to automatically synthesize a controller that implements this behavior. Controller synthesis is complicated by the fact that autonomous systems often have high-dimensional, nonlinear dynamics and require efficient (not just feasible) controllers.

This project aims at designing a “correct by construction” controller for an autonomous vehicle that is capable of responding to a dynamic environment, visiting goals, periodically monitoring areas, staying safe, and remaining stable. To this end, we will take advantage of the new tools and techniques for formal specification, design, and verification of embedded control systems [3,4,5,7]. In these approaches, we either verify that a given design satisfies the specification or synthesize a controller that satisfies the specification, as summarized in the following figure.

The formal language that we use in this project is Signal Temporal Logic (STL), which allows the specification of properties of dense-time, real-valued signals. For an efficient implementation, we will directly encode an STL formula as mixed-integer linear constraints on the original dynamical system [6]. Of particular interest are mixed logical dynamical (MLD) systems and certain differentially flat systems [2], whose dynamics can be encoded with mixed-integer linear constraints. MLD systems include constrained linear systems, linear hybrid automata, and piecewise affine systems. Differentially flat systems include quadrotors and car-like robots.

After the successful design the controller, we are going to perform a detailed comparison of mixed-integer linear programming solvers and Boolean satisfiability solvers that have been extended to support linear operations, e.g., [1]. Moreover, depending on the progress lever, we can also implement the controller on of the available robots in the lab for experimental purposes.

Agent.png

Required Skills: The software we will use for the implementation of formal methods is called TuLiP [5] and the programming language underlying TuLiP is Python. The student is expected to know Matlab and Python or to have enough programming experience to learn it in a short time. Some familiarity with or willingness to learn automata theory, formal languages, and model checking (see for instance to the extent of the first 5 lectures in [6]) is desired.

References:

[1] M. Fränzle and C. Herde. Efficient proof engines for bounded model checking of hybrid systems. Electronic Notes in Theoretical Computer Science, 133:119–137, 2005. http://homepage.divms.uiowa.edu/~tinelli/classes/AR-group/readingsF04/FMICS04_Fraenzle_Herde.pdf

[2] S. M. LaValle. Planning Algorithms. Cambridge Univ. Press, 2006. http://planning.cs.uiuc.edu/bookbig.pdf

[3] S. Livingston, R. M. Murray, and J. W. Burdick. Backtracking temporal logic synthesis for uncertain environments. In Proc. IEEE International Conference on Robotics and Automation, 2012. http://scottman.net/pub/Livingston-Murray-Burdick-ICRA2012.pdf

[4] U. Topcu, N. Ozay, J. Liu, , and R. M. Murray. On synthesizing robust discrete controllers under modeling uncertainty. In Hybrid Systems: Computation and Control, 2012. http://www.cds.caltech.edu/~murray/preprints/tolm12-hscc_s.pdf

[5] E. M. Wolff, U. Topcu, and R. M. Murray, Optimization-based trajectory generation with linear temporal logic specifications, International Conference on Robotics and Automation (ICRA), 2014. http://www.cds.caltech.edu/~ewolff/wolff_icra14.pdf

[6] V. Raman, A. Donzé, M. Maasoumy, R. M. Murray, A. Sangiovanni-Vincentelli, S. A. Seshia, Model Predictive Control with Signal Temporal Logic Specifications, CDC 2014. http://users.cms.caltech.edu/~vasu/papers/vraman_cdc_14.pdf

[7] T. Wongpiromsarn, U. Topcu, and R. M. Murray. Receding horizon temporal logic planning. IEEE Transactions on Automatic Control, 57(11):2817{2830, 2012. http://www.seas.upenn.edu/~utopcu/pubs/WTM-itac12.pdf

[8] Wongpiromsarn, U. Topcu, N. Ozay, H. Xu, and R.~M. Murray, TuLiP: a software toolbox for receding horizon temporal logic planning, International Conference on Hybrid Systems: Computation and Control, 2011 (software available at http://tulip-control.sourceforge.net). http://www.aero.umd.edu/~mumu/files/wtoxm_HSCC2011.pdf

[9] EECI, "Specification, Design, and Verification of Distributed Embedded Systems" course website http://www.cds.caltech.edu/~murray/wiki/index.php/HYCON-EECI,_Spring_2013

Retrieved from "https://murray.cds.caltech.edu/index.php?title=SURF_2015:_Optimal_Trajectory_Generation_under_Environmental_Uncertainties_using_Signal_Temporal_Logic_Specifications&oldid=17895"