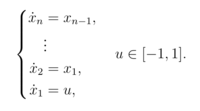SURF 2019: Geometry of Control-Invariant Sets: Difference between revisions

From Murray Wiki
Jump to navigationJump to search
No edit summary
mNo edit summary
 
(3 intermediate revisions by 2 users not shown)
Line 1: Line 1:
'''[[SURF 2019|2019 SURF]]: project description'''
* Mentor: Richard M. Murray
* Co-mentor: Petter Nilsson
The concept of a ''control-invariant'' set---a set <math>X</math> with the property that a controller can make the state <math>x(t)</math> of a system remain inside of <math>X</math> for all positive <math>t</math> ---is closely connected with safety and reliability of engineered systems [1]. Invariant sets can be used to construct controllers that make systems such as quadrotors avoid crashes [2]. Unfortunately, analytical expressions for control-invariant sets are not known for many important systems, and are also hard to compute numerically in high dimensions.  
The concept of a ''control-invariant'' set---a set <math>X</math> with the property that a controller can make the state <math>x(t)</math> of a system remain inside of <math>X</math> for all positive <math>t</math> ---is closely connected with safety and reliability of engineered systems [1]. Invariant sets can be used to construct controllers that make systems such as quadrotors avoid crashes [2]. Unfortunately, analytical expressions for control-invariant sets are not known for many important systems, and are also hard to compute numerically in high dimensions.  


[[File:Double_int.png]] [[File:Triple_int.png]]
[[File:Double_int.png|350px]] [[File:Triple_int.png|350px]]
 
Some of the most fundamental dynamical systems are linear <math>n</math>-order integrators:
 
[[File:N_integrator.png|200px]]


Some of the most fundamental dynamical systems are linear <math>n</math>-order integrators. For <math>n</math> = 2 a closed-form expression of the maximal control-invariant set contained inside the unit hypercube is known [3. eq. (53)], but for higher orders of <math>n</math> only numerical approaches are available. The figures above show numerical approximations for <math>n</math> equal to 2 and <math>n</math> equal to 3. The objective of this project is to investigate geometrical properties of control-invariant sets via a combination of analytical and numerical techniques. In particular,
For <math>n</math> = 2 a closed-form expression of the maximal control-invariant set contained inside the unit hypercube is known [3. eq. (53)], but for higher orders of <math>n</math> only numerical approaches are currently available. The figures above show numerical approximations for <math>n</math> equal to 2 and <math>n</math> equal to 3.  


The objective of this project is to investigate geometrical properties of control-invariant sets via a combination of analytical and numerical techniques. In particular,
* Search for closed-form expressions or cheap-to-evaluate algorithms that characterize control-invariant sets for n > 2.
* Search for closed-form expressions or cheap-to-evaluate algorithms that characterize control-invariant sets for n > 2.
* Investigate incremental algorithms, i.e., if the set for n is known, can we characterize the set for n+1?
* Investigate incremental algorithms, i.e., if the set for n is known, can we characterize the set for n+1?
Line 10: Line 19:


Familiarity with the following topics is desirable:
Familiarity with the following topics is desirable:
* Advanced knowledge of linear ordinary differential equations.
* Advanced knowledge of linear ordinary differential equations.
* Optimization.
* Optimization.

Latest revision as of 03:40, 28 November 2018

2019 SURF: project description

  • Mentor: Richard M. Murray
  • Co-mentor: Petter Nilsson

The concept of a control-invariant set---a set with the property that a controller can make the state of a system remain inside of for all positive ---is closely connected with safety and reliability of engineered systems [1]. Invariant sets can be used to construct controllers that make systems such as quadrotors avoid crashes [2]. Unfortunately, analytical expressions for control-invariant sets are not known for many important systems, and are also hard to compute numerically in high dimensions.

Double int.png Triple int.png

Some of the most fundamental dynamical systems are linear -order integrators:

N integrator.png

For = 2 a closed-form expression of the maximal control-invariant set contained inside the unit hypercube is known [3. eq. (53)], but for higher orders of only numerical approaches are currently available. The figures above show numerical approximations for equal to 2 and equal to 3.

The objective of this project is to investigate geometrical properties of control-invariant sets via a combination of analytical and numerical techniques. In particular,

  • Search for closed-form expressions or cheap-to-evaluate algorithms that characterize control-invariant sets for n > 2.
  • Investigate incremental algorithms, i.e., if the set for n is known, can we characterize the set for n+1?
  • Stretch goal: generalize the incremental ideas to differential extensions of general systems such as the quadrotor dynamics on SE(3).

Familiarity with the following topics is desirable:

  • Advanced knowledge of linear ordinary differential equations.
  • Optimization.
  • Programming in Matlab and/or Python (the figures above were created with code from https://github.com/pettni/pcis).

References

[1] Blanchini, F. (1999). Set invariance in control. Automatica, 35(11), 1747–1767. https://doi.org/10.1016/S0005-1098(99)00113-2

[2] https://www.youtube.com/watch?v=rK9oyqccMJw

[3] Ames, A. D., Xu, X., Grizzle, J. W., & Tabuada, P. (2017). Control Barrier Function Based Quadratic Programs for Safety Critical Systems. IEEE Transactions on Automatic Control, 62(8), 3861–3876. https://doi.org/10.1109/TAC.2016.2638961

Retrieved from "https://murray.cds.caltech.edu/index.php?title=SURF_2019:_Geometry_of_Control-Invariant_Sets&oldid=22255"