Information and Decision Systems

PhD Program/Graduate Minor in Information and Decision Systems (IDS)

Mani Chandy    John Doyle    Michelle Effros    Babak Hassibi    Tracey Ho    Andreas Krause    Steven Low    Richard Murray    Joel Tropp    Adam Wierman    Erik Winfree

Executive Summary

We propose to establish a new graduate program at Caltech in Information and Decision Systems (IDS). The program will consist of both a PhD program intended to attract exceptional students from around the world and graduate minor for students in existing options wishing to concentrate in this area. The intent of both programs is to provide students with a strong education in the mathematical techniques and insights required for the study of large-scale, complex, networked, information and decision systems in a variety of areas of science and engineering. The program is structured to leverage Caltech's strengths in science, mathematics and engineering, and the interests of faculty around the campus to develop fundamental tools for helping unravel the complexity of biological, chemical, economic, information, physical and social systems. The program will be administered by a small, core group of faculty, but students are expected to work with faculty from around the campus to help promote interdisciplinary studies.

Motivation: The Future of Complex Systems Research

Many cutting edge problems in the natural sciences involve understanding aggregate behavior in complex large-scale systems. This behavior "emerges" from the interaction of a large number of simpler systems, with intricate patterns of information flow. Representative examples can be found in fields ranging from embryology to seismology to global climate change. Key features of these new challenges include the (sometimes bewildering) complexity of the underlying phenomena of interest, the increasing ability to collect large amounts of data from sophisticated instruments, and the desire to develop principles that aid in our understanding and allow us to predict future behavior and/or design systems that behave reliably in the presence of large amounts of uncertainty.

While sophisticated theories have been developed by domain experts for the analysis of various complex systems, the development of rigorous methodology that can discover and exploit common features and essential mathematical structure remains a major challenge to the research community; we need new approaches and techniques.

To address this opportunity, we believe that a new PhD program in Information and Decision Systems is timely and would keep Caltech in a leadership position in fundamental research on complex, networked information and decision systems across several areas of applied science and mathematics in which Caltech is already active, as well as enable potentially new thrusts within the sciences. The long term goals of this PhD program are to:

• develop new approaches for understanding and building complex information and decision systems, with an emphasis on the underlying theory and application across a broad variety of the sciences and engineering.

• recruit students, postdocs and faculty to Caltech who will serve as leaders in their respective fields around the world, and who will help develop the theoretical frameworks required to tackle new problems in complex, networked systems.

• develop a curriculum and educational culture that supports the education of broadly-trained scientists, applied mathematicians and engineers who work in and across multiple disciplines over the course of their careers.

A key theme of the program is to help facilitate interaction between a broad variety of application areas in which in a common set of mathematical problems arise. This will be accomplished in part by keeping the program very open and encouraging students to work with faculty from around the campus. Some examples of application areas where we believe IDS students could contribute:

• Next generation infrastructure networks (smart grid, air traffic control)
• Next generation sensor networks (Trinet)

Structure of the Program

The overall structure of the program reflects the interdisciplinary nature of the research that will drive it forward, as well as the multiple channels for students, postdocs and faculty that will make up the program. On the one hand, the program is intended to bring together a network of people that will interact with each other to work on problems of fundamental scientific and mathematical importance. On the other hand, the program reflects an interaction between a variety of different application areas and underlying disciplines and must be structured to facilitate communications across this diverse intellectual backdrop.

Program architecture

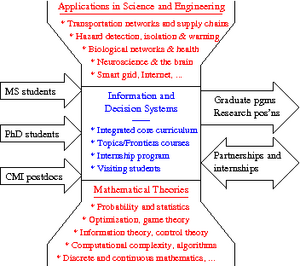
In the study of complex systems, a key element is the development of architectures that allow us to understand common principles between different phenomena and also rapidly exploit these principles to facilitate the exchange of ideas and advances in underlying mathematical techniques. The figure to the right shows the basic architecture of the program.

Going from top to bottom is the intellectual ``hourglass that reflects the role of the program in linking mathematical techniques to scientific applications. The intent is not to argue that the \phdabbv program is at the center of the world, but rather to describe the drivers of the program as coming from new mathematical theories and techniques combined with insights and challenges coming from a diverse set of scientific challenges and opportunities. The success of the program will depend on the ability to identify a coherent set of intellectual themes that can help facilitate these interactions and that add value to research in both the mathematical core and the application sciences.

The left to right flow across the diagram represents the flow of people into and out of the program. As we envision it, the program will be rooted in a standard 4-5 year PhD program that brings in students from a variety of external universities and prepares them for intellectual leadership position in academic and industry. In addition, we propose to establish a graduate minor that allows students from other Caltech options to learn the theory and tools that may be relevant for their research interests. Finally, we hope to build off of the successful CMI postdoc program and include postdocs who received their PhDs from other universities who come to Caltech for two years of independent research, working with faculty from around the campus.

PhD program

The PhD program will serve as the core of the educational program and provide a common collection of fundamental tools that can be used as a starting point for research. The following courses will be required of all students enrolled in the PhD program:

• Core courses: IDS 110 (linear algebra and optimization), IDS 120 (stochastic systems), IDS 130 (information systems), IDS 140 (data-driven modeling), IDS 150 (decision making systems)
• Exploratory courses: IDS 210 (Frontiers), IDS 220 (Topics), IDS 230 (Reading)
• Focus requirement: three quarters of graduate course work in any area of science, engineering or mathematics

The core course work will be done in the first year, with a few more specialized courses in the second year. Courses in the first and second term would consist of fundamental course work that would be taken by all PhD students and would provide the common mathematical background required for research in IDS. The third term would be used for teaching more advanced topics that would change from year to year. In addition, the third term would contain two new courses, the ``Frontiers and ``Topics courses.

Core Courses

Track	Fall	Winter	Spring
Optimization and linear algebra IDS 110ab	ACM 104/CDS 201 (Beck, Murray, Owhadi) Perhaps rename this row "Linear algebra and optimization" Similar course at MIT	ACM 113 (Doyle, Owhadi, Tropp) Convex analysis Linear programming/duality	Decision making IDS 150 (Doyle, Low, Murray) Dynamics and stability Nonlinear discrete time systems, hybrid systems Stability and stability certificates (Lyapunov, SOS) Feedback systems, small gain theorems Uncertainty and robustness Representation of uncertainty Operator bounds; links to small gain Robust performance: discrete time, NL? Need to say all of this in a non-control specific way Fundamental limits: Bode, Shannon, Bode/Shannon Case studies Internet: layering as optimization One more (not the cell)
Stochastic systems IDS 120ab	ACM/EE 116 (Hassibi, Owhadi, Tropp) Introduction to Stochastic Processes and Modeling	ACM 216 (Owhadi, Tropp) Markov Chains, Discrete Stochastic Processes and Applications
Information systems IDS 130ab	CS/EE/Ma 129a (Abu-Mostafa, Winfree) Information and complexity Information theory and coding Finite state automata, Turing machines, computability Data compression Note: EE 126 is an alternative to this course for people who have already seen automata, computability, etc	CS/EE/Ma 129b (Abu-Mostafa, Winfree) Information and complexity Channel coding, capacity and rate theorem Time complexity of algorithms; P vs NP Formal logic and provability
Data-driven modeling IDS 140ab	CS/CNS/EE 156 (Abu-Mostafa, Krause) Learning systems	CS 155 (Krause) Graphical models